PPT Introducción a la Derivada PowerPoint Presentation, free download ID5233460
La relación gráfica entre una función y su derivada (parte 2) Google Classroom. Acerca de. Transcripción. Dada la gráfica de una función, bosquejamos la gráfica de su antiderivada. En otras palabras, bosquejamos la gráfica de la función cuya derivada es la función dada. Creado por Sal Khan.
Representación gráfica de las derivadas YouTube

Representación gráfica de una Derivada. Autor: Alejandro Kentros. Tema: Cálculo, Derivada, Cálculo diferencial, Matemática
Presentación

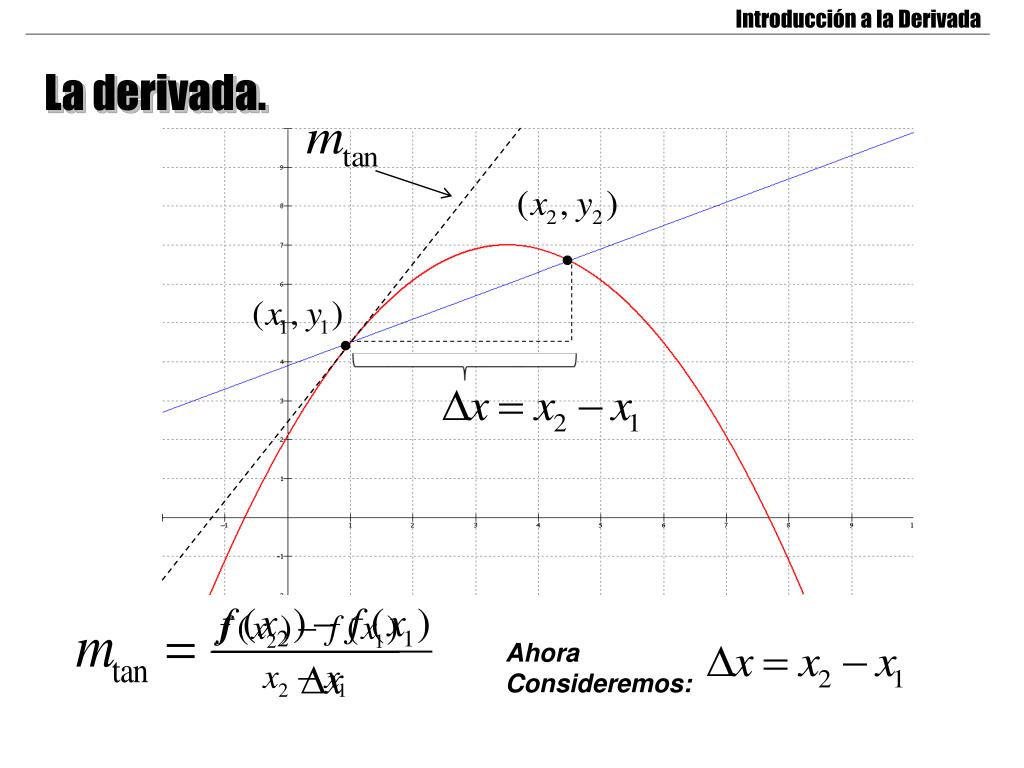
Si cada vez que avanzas en la x la pendiente baja una cantidad constante, la función de arriba sube cada vez más despacio, pero sigue subiendo hasta que la pendiente es 0, si la derivada es lineal es que las rectas tangentes en cada punto de la función tienen una PENDIENTE cada vez menor, de forma constante, por eso sale una curva del tipo -x^2, cada vez deja de subir con mayor intensidad.
¿Se pueden entender las matemáticas? El concepto de derivada de una función
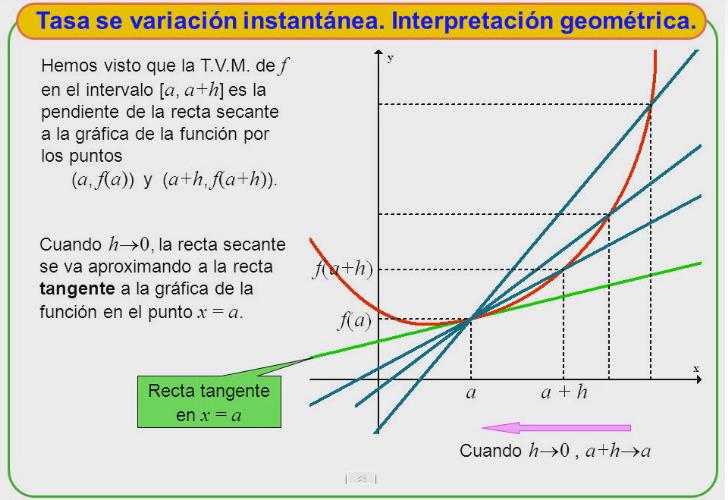
La segunda derivada, a su vez, puede representar la aceleración. ¡Gira esa curva, que aquí viene la guía para hacer una representación gráfica de la derivada! Agárrate bien al lápiz y prepárate para dibujar como un verdadero matemático loco. Primero, toma tu función y dale un abrazo bien apretado.
Criterios de la segunda derivada
Definición. Supongamos que f es una función. La función derivada, denotada por f ′, es la función cuyo dominio consiste en los valores de x de manera tal que el siguiente límite existe: f ′ (x) = lím h → 0f(x + h) − f(x) h. (3.9) Una función f(x) se dice que es diferenciable en a si f ′ (a).
Derivadas Unidad de Apoyo Para el Aprendizaje
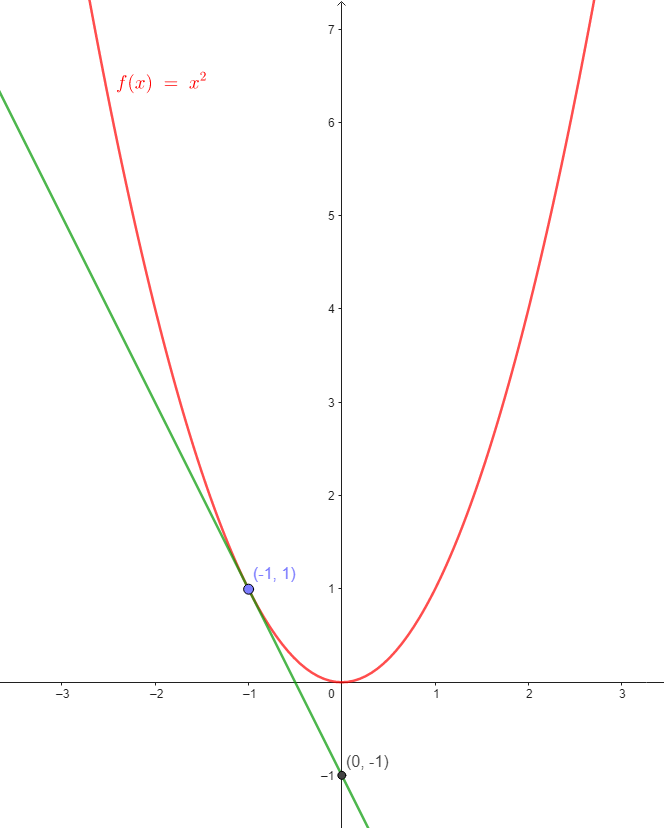
Una de las partes más fundamentales del cálculo es que la derivada de cualquier punto es igual a la tangente de la curva en ese punto. Entonces, cuando volvemos a Super C, la tangente de su altura en función del tiempo, y en cualquier punto a lo largo de esa curva, es igual a la derivada en ese punto. Si encontramos donde la derivada es.
La derivada como pendiente de una curva AP Cálculo BC Khan Academy en Español YouTube
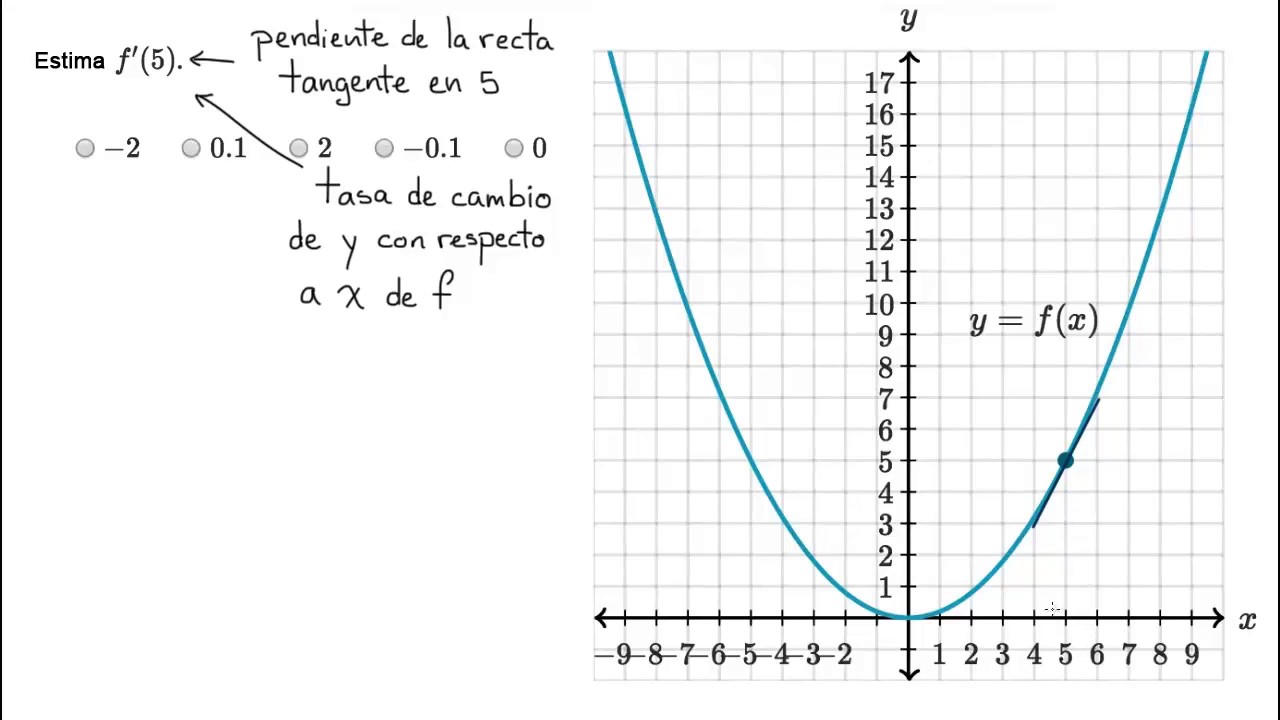
La derivada de una función describe la razón de cambio instantáneo de la función en un cierto punto. Otra interpretación común es que la derivada nos da la pendiente de la recta tangente a la gráfica de la función en ese punto. Aprende cómo definimos la derivada mediante límites. Conoce un conjunto de reglas muy útiles (como las reglas de potencia, producto y cociente) que nos.
Representación gráfica de una Derivada GeoGebra

Definición: Derivada. Let f(x) Ser una función definida en un intervalo abierto conteniendo a. La derivada de la función f(x) at a, denotada por f′ (a), se define por. f′ (a) = lim x → a f(x) − f(a) x − a. siempre y cuando este límite exista. Alternativamente, también podemos definir la derivada de f(x) at a como.
Tema4 Derivada de la gráfica de la función a la derivada. YouTube

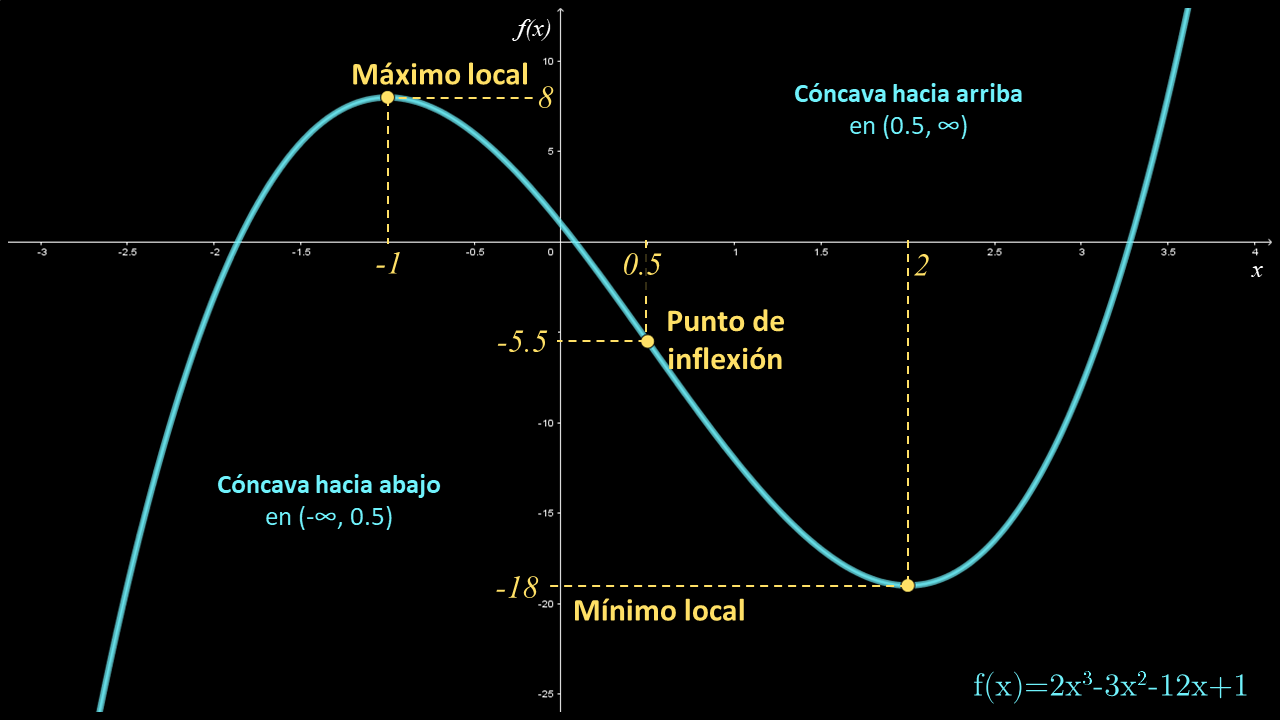
Objetivos de aprendizaje. 4.5.1 Explicar cómo el signo de la primera derivada afecta a la forma del gráfico de una función.; 4.5.2 Enunciar la prueba de la primera derivada para los puntos críticos.; 4.5.3 Utilizar la concavidad y los puntos de inflexión para explicar cómo el signo de la segunda derivada afecta a la forma del gráfico de una función.
DERIVADA Interpretación gráfica y algunas de sus aplicaciones. YouTube

En cada punto x, la derivada f ' ( x) > 0. (c) y (d) Ambas funciones están disminuyendo a lo largo del intervalo ( a, b ). En cada punto x, la derivada f ' ( x) < 0. Una función continua f tiene un máximo local en el punto c si y solo si f cambia de creciente a de creciente en el punto c. De manera similar, f tiene un mínimo local en c.
Cálculo gráfico de derivadas GeoGebra
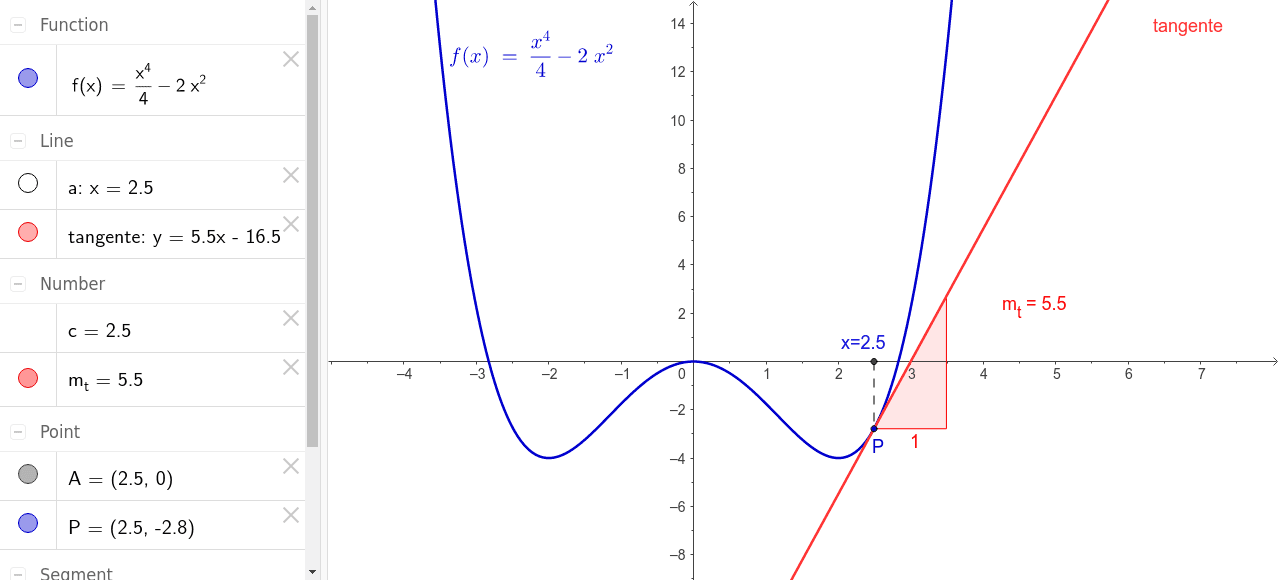
Mediante un gráfico animado se muestra la interpretación gráfica de la derivada , así como algunas de sus aplicaciones.#MateSimple
PPT Tema 3. La Derivada. Aplicaciones y representación gráfica de funciones PowerPoint

Graficador de Derivadas. ¡Diviértete con las derivadas ! Escribe una función y observa su pendiente (calculada por el programa). Luego mira si puedes averiguar la derivada tú mismo. Grafica tu función en azul, y traza la pendiente de la función en el gráfico siguiente en rojo (el graficador calcula la diferencia entre cada punto en la.
Conociendo las funciones y sus derivadas Contenido de Funciones y Derivadas

gráficas de la derivada. La derivada como ya hemos visto nos sirve para determinar la velocidad instantánea de cambio de una función en un punto y resulta numéricamente igual al valor de la pendiente de la recta tangente a la función en el punto en que se evalúa. Por tanto nos sirve para encontrar rectas tangentes y normales a curvas dadas.
Derivadas. interpretación Geometrica de la derivada. Cálculo Diferencial. YouTube

Conceptos clave. La derivada de una función es la función cuyo valor at es. La gráfica de una derivada de una función está relacionada con la gráfica de. Donde tiene una línea tangente con pendiente positiva,. Donde tiene una línea tangente con pendiente negativa,.
Derivando DERIVADA DE UNA FUNCIÓN EN UN PUNTO

Interpretación geométrica del concepto de derivada: Moviendo el punto A, se puede observar como va variando la pendiente de la recta tangente a la curva, simultáneamente el punto B va dejando un rastro asociado a este valor,que es precisamente la construcción de la función derivada. Observa la diferencia: el valor de la función derivada.
Calculando la derivada de la función 3x^2+12 con límites. Ejemplo 1 YouTube

Utilice la primera prueba derivada para encontrar la ubicación de todos los extremos locales para f(x) = x3 − 3x2 − 9x − 1. Use una utilidad gráfica para confirmar sus resultados. Solución. Paso 1. La derivada es f ′ (x) = 3x2 − 6x − 9. Para encontrar los puntos críticos, necesitamos encontrar donde f ′ (x) = 0.
.

